
 Top of Part 3
Top of Part 3

 Last page
Last page

 Next page
Next page
  Top of Part 3
Top of Part 3
  Last page
Last page
  Next page
Next page
|
3-4: Planck's Formula |
 On the preceding page, On the preceding page,
 we studied about we studied about
 the heat capacity of the heat capacity of
 a cavity a cavity
 or a vacuum. or a vacuum.
 The result said that, The result said that,
 if we naively apply if we naively apply
 the law of equipartition the law of equipartition
 of energy, of energy,
 the total energy the total energy
 of a vacuum (cavity) of a vacuum (cavity)
 becomes infinite. becomes infinite.
 This is completely This is completely
 different from the reality. different from the reality.

 Is the law Is the law
 of equipartition of energy of equipartition of energy
 inapplicable for the inapplicable for the
 cavity radiation? cavity radiation?
 The law is naturally derived The law is naturally derived
 from the classical theory from the classical theory
 consisting of consisting of
 Newtonian mechanics Newtonian mechanics
 and Maxwellian electromagnetism. and Maxwellian electromagnetism.
 This seems to suggest This seems to suggest
 that there must that there must
 be something wrong be something wrong
 in the classical theories. in the classical theories.
 Then, where is the secret hidden? Then, where is the secret hidden?
 This is one This is one
 of the biggest problems of the biggest problems
 in physics at the end in physics at the end
 of the 19th century. of the 19th century.

|
 [Rayleigh-Jeans's Formula] [Rayleigh-Jeans's Formula]

 As discussed As discussed
 on the preceding page, on the preceding page,
 Maxwellian electromagnetism Maxwellian electromagnetism
 gives the gives the
 number of number of
 the normal oscillations the normal oscillations
 with the frequency with the frequency
 between between

 and and

 per unit volume as per unit volume as




 If the constant energy kT If the constant energy kT
 is partitioned is partitioned
 to all these normal oscillations to all these normal oscillations
 according to the according to the
 law of equipartition law of equipartition
 of energy, of energy,
 then the energy then the energy
 of the radiation (or light) of the radiation (or light)
 with the frequencies with the frequencies
 between between

 and and

 per unit volume becomes per unit volume becomes




 This is the Rayleigh-Jeans This is the Rayleigh-Jeans
 formula formula
 proposed by proposed by
 J. W. S. Rayleigh J. W. S. Rayleigh
 (UK, 1842 - 1919) (UK, 1842 - 1919)
 and and
 J. H. Jeans J. H. Jeans
 (UK, 1877 - 1946). (UK, 1877 - 1946).

 If we measure the frequencies If we measure the frequencies
 and intensities of and intensities of
 lights existing lights existing
 inside a high-temperature inside a high-temperature
 space like a blast furnace space like a blast furnace
 in an iron industry, in an iron industry,
 we can obtain we can obtain
 the spectrum the spectrum
 (intensity distribution (intensity distribution
 for each frequency of light). for each frequency of light).
 The experimental data The experimental data
 are shown in the following are shown in the following
 figure. figure.

|

|
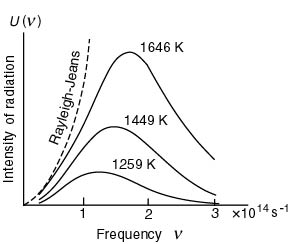
 Experimental spectra of the cavity radiation
Experimental spectra of the cavity radiation

 The positions of The positions of
 the hill tops the hill tops
 of the solid curves of the solid curves
 on the horizontal axis on the horizontal axis
 denote the frequency denote the frequency
 of the brightest light. of the brightest light.
 As the absolute temperature As the absolute temperature
 T of each curve T of each curve
 becomes high, becomes high,
 the frequency the frequency
 of the brightest light of the brightest light
 shifts gradually to higher. shifts gradually to higher.
 This means This means
 that the color that the color
 of cavity changes of cavity changes
 from red from red
 to white, to white,
 as the temperature as the temperature
 becomes higher. becomes higher.
 The dashed curve The dashed curve
 shows the values shows the values
 of Rayleigh-Jeans's formula of Rayleigh-Jeans's formula
 for T = 1646 K. for T = 1646 K.

|
 For example, For example,
 when heating up when heating up
 an iron block, an iron block,
 the color of the ion the color of the ion
 is gray is gray
 at a low temperature. at a low temperature.
 It would be bright red It would be bright red
 at about at about

 and become white and become white
 and dazzling at and dazzling at

 This feature This feature
 is shown in is shown in
 the above figure. the above figure.

 In the above figure, In the above figure,
 the values of the values of
 the Rayleigh-Jeans formula the Rayleigh-Jeans formula
 are shown by a are shown by a
 dashed curve. dashed curve.
 It is well fit It is well fit
 to experimental data to experimental data
 at low frequencies, at low frequencies,
 but becomes worse but becomes worse
 at high frequency. at high frequency.
 This appears to imply that This appears to imply that
 the law of equipartition the law of equipartition
 of energy of energy
 is not valid is not valid
 for high frequencies. for high frequencies.

|
 [Wien's Formula] [Wien's Formula]

 W. Wien W. Wien
 (Germany, 1864 - 1928) (Germany, 1864 - 1928)
 extended a very ingenious extended a very ingenious
 discussion of generality discussion of generality
 to obtain a formula to obtain a formula
 describing the intensity describing the intensity
 distribution distribution
 in the cavity radiation in the cavity radiation
 (1896). (1896).
 Since Wien's idea Since Wien's idea
 is somewhat difficult is somewhat difficult
 to explain simply, to explain simply,
 we omit it and represent we omit it and represent
 only the result here. only the result here.

 According to Wien, According to Wien,
 the energy distribution the energy distribution
 of the cavity radiation of the cavity radiation
 for a unit volume for a unit volume
 is given by is given by




 We cannot obtain We cannot obtain
 the form of the function the form of the function
 F(x) F(x)
 only from Wien's discussion. only from Wien's discussion.
 However the most important However the most important
 is that is that
 the functional value the functional value
 is determined only by is determined only by
 the ratio of the frequency the ratio of the frequency

 to the temperature to the temperature
 T . T .
 This is quite well fit This is quite well fit
 to experiment. to experiment.
 This law is called This law is called
 Wien's law Wien's law
 (or Wien's displacement law). (or Wien's displacement law).

 Let the wave length Let the wave length
 of the brightest light of the brightest light
 in the cavity radiation be in the cavity radiation be
 . .
 Differentiating the above Differentiating the above
 Wien's law by Wien's law by

 we can easily obtain we can easily obtain




 This is often called This is often called
 Wien's displacement law. Wien's displacement law.

 Setting Setting
 F(x) = k/x F(x) = k/x
 in Wien's law, in Wien's law,
 we have we have
 the Rayleigh-Jeans formula. the Rayleigh-Jeans formula.

 Wien took Wien took




 and obtained Wien's formula and obtained Wien's formula




 If the constant If the constant

 is adjusted is adjusted
 to an appropriate value, to an appropriate value,
 the values of the values of
 Wien's formula Wien's formula
 are well fit to are well fit to
 the experimental data the experimental data
 at the high-frequency region. at the high-frequency region.

|
 [Planck's Formula] [Planck's Formula]

 As discussed above, As discussed above,
 the Rayleigh-Jeans formula the Rayleigh-Jeans formula
 concerning the cavity radiation concerning the cavity radiation
 gives very good fit gives very good fit
 to experiment to experiment
 in the low frequency region. in the low frequency region.
 On the other hand, On the other hand,
 Wien's formula Wien's formula
 is very good is very good
 in the high in the high
 frequency region. frequency region.
 Then, M.K.E.L. Planck Then, M.K.E.L. Planck
 (Germany, 1858 - 1947) (Germany, 1858 - 1947)
 proposed an interpolating formula proposed an interpolating formula
 which can unify which can unify
 these two formulae these two formulae
 and and
 brings about very brings about very
 good fit to experiment over good fit to experiment over
 all regions of frequencies. all regions of frequencies.
 This is the famous This is the famous
 Planck's formula Planck's formula
 which is which is
 one of the biggest discoveries one of the biggest discoveries
 at the end of the 19th century. at the end of the 19th century.

 Planck proposed Planck proposed
 that the function F(x) that the function F(x)
 in the above mentioned in the above mentioned
 Wien's law Wien's law
 should be taken as should be taken as




 Accordingly, the energy Accordingly, the energy
 distribution in the cavity distribution in the cavity
 radiation becomes radiation becomes




 This is Planck's formula, This is Planck's formula,
 and the constant k and the constant k
 is Boltzmann's constant is Boltzmann's constant
 that is a universal constant, that is a universal constant,




 Another constant Another constant

 is adjustable, is adjustable,
 which which
 is usually written is usually written
 , ,
 where where
 h is called h is called
 Planck's constant Planck's constant
 whose value whose value
 is given as is given as




 You can easily see in You can easily see in
 the following figure the following figure
 how well Planck's formula how well Planck's formula
 reproduces reproduces
 the experimental data. the experimental data.

|


|
 Comparison between Comparison between
 the experimental the experimental
 spectrum of the spectrum of the
 cavity radiation cavity radiation
 and Planck's formula. and Planck's formula.

 The small circles The small circles
 are experimental data are experimental data
 and the solid and the solid
 curves denote curves denote
 the values of the values of
 Planck's formula. Planck's formula.
 Be careful the Be careful the
 abscissa abscissa
 shows the wave length, shows the wave length,
 not the frequency. not the frequency.

|
 [Comparison between
the Three Formulae] [Comparison between
the Three Formulae]

 As discussed above, As discussed above,
 Rayleigh-Jeans's formula Rayleigh-Jeans's formula
 shows a good fit shows a good fit
 to experiment to experiment
 in the low-frequency region in the low-frequency region
 and Wien's formula and Wien's formula
 is good in the is good in the
 high-frequency region. high-frequency region.
 Planck's formula Planck's formula
 can reproduce the experimental can reproduce the experimental
 energy distribution energy distribution
 throughout all frequency regions. throughout all frequency regions.

 A comparison between A comparison between
 these three formulae these three formulae
 is given is given
 in the following figure. in the following figure.
 You can see You can see
 from this figure that from this figure that
 Planck's formula Planck's formula
 is just an interpolation is just an interpolation
 of Rayleigh-Jeans's formula of Rayleigh-Jeans's formula
 and Wien's formula. and Wien's formula.

|


|

 Comparison between Comparison between
 Rayleigh-Jeans's, Rayleigh-Jeans's,
 Wien's Wien's
 and and
 Planck's formula Planck's formula

|
 Top
Top
|
|

 Go back to
the top page of Part 3. Go back to
the top page of Part 3.

 Go back to
the last page. Go back to
the last page.

 Go to
the next page. Go to
the next page.
|