
 Top of Part 3
Top of Part 3

 Last page
Last page

 Next page
Next page
  Top of Part 3
Top of Part 3
  Last page
Last page
  Next page
Next page
|
3-2: Molecular Motions and Heat Capacities |
 The quantity The quantity
 of heat required of heat required
 to raise the temperature to raise the temperature
 of a substance of a substance
 by by


 is called is called
 heat capacity; heat capacity;
 especially for 1 g especially for 1 g
 of the substance, of the substance,
 it is called it is called
 specific heat capacity specific heat capacity
 or or
 specific heat. specific heat.
 (The adjective (The adjective
 specific means specific means
 "per unit mass".) "per unit mass".)
 For example, For example,
 since the heat since the heat
 necessary to warm up necessary to warm up
 1 g of water by 1 g of water by


 is 1 cal, is 1 cal,
 the specific heat the specific heat
 of water is of water is




 If such a physical If such a physical
 quantity quantity
 in the macroscopic in the macroscopic
 world as specific heat world as specific heat
 can be derived can be derived
 from the molecular from the molecular
 or atomic degrees of freedom or atomic degrees of freedom
 in the microscopic world, in the microscopic world,
 how wonderful how wonderful
 it would be! it would be!
 To explain this, To explain this,
 let us study let us study
 the law of the law of
 equipartition of energy. equipartition of energy.




|
 [The Law of Equipartition of Energy] [The Law of Equipartition of Energy]


 When we learned When we learned
 about the motion about the motion
 of molecules on the page,
1-4:
The Motion of Molecules, of molecules on the page,
1-4:
The Motion of Molecules,
 we estimated we estimated
 the speed the speed
 of the molecules of the molecules
 in a gas. in a gas.
 There, There,
 putting a gas putting a gas
 in a cubic container in a cubic container
 as shown as shown
 in Fig. (A) in Fig. (A)
 and and
 assuming the x -component assuming the x -component
 of the average velocity of the average velocity
 of the molecule of the molecule
 to be to be
 vx ,
vx ,

 we calculated the pressure we calculated the pressure
 applied onto the wall A applied onto the wall A
 of the container. of the container.
 Consequently, we obtained Consequently, we obtained
 a relation a relation



 where P, where P,
 V and M V and M
 are the pressure, are the pressure,
 the volume and the the volume and the
 total mass of the gas, total mass of the gas,
 respectively. respectively.

 Now, consider Now, consider
 1 mole of gas. 1 mole of gas.
 Let m be Let m be
 the mass of a single molecule the mass of a single molecule
 and T the absolute and T the absolute
 temperature of the gas. temperature of the gas.
 The total mass The total mass
 of the gas of the gas
 is M = m NA, is M = m NA,
 where NA where NA
 is the Avogadro constant. is the Avogadro constant.
 Combining the above relation and Combining the above relation and
 famous Boyle-Charles's law famous Boyle-Charles's law



 we have we have



 Here Here
 k is k is
 a fundamental constant a fundamental constant
 called called
 the Boltzmann constant. the Boltzmann constant.

 The quantity The quantity

 on the left-hand side on the left-hand side
 of the above equation of the above equation
 is the kinetic energy is the kinetic energy
 of a molecule. of a molecule.
 This implies This implies
 that the mean value that the mean value
 of the kinetic energy of the kinetic energy
 of one molecule is kT /2. of one molecule is kT /2.

 In this discussion, In this discussion,
 we consider we consider
 that the molecular motion that the molecular motion
 is only in the is only in the
 x direction. x direction.
 In a realistic case, In a realistic case,
 a molecule has also a molecule has also
 the y- and the y- and
 z-components z-components
 of the velocity. of the velocity.
 Let the Let the
 x- , x- ,
 y- y-
 and z-components and z-components
 of the average molecular velocity of the average molecular velocity
 be be
 vx , vx ,
 vy , vy ,
 and and
 vz vz
 respectively. respectively.
 Then the Then the
 average kinetic energy average kinetic energy
 of the molecule, of the molecule,
 , ,
 is written is written



 This result tells us This result tells us
 that the mean value that the mean value
 of the kinetic energy of of the kinetic energy of
 each degree of freedom each degree of freedom
 in the in the
 x, x,
 y and z y and z
 directions directions
 is kT /2. is kT /2.
 In other words, In other words,
 the equal amount of energy the equal amount of energy
 kT /2 kT /2
 is distributed to is distributed to
 each of all the degrees each of all the degrees
 of freedom of the molecules. of freedom of the molecules.
 This is called This is called
 the law the law
 of equipartition of energy. of equipartition of energy.

 According to the According to the
 theories of theories of
 statistical mechanics, statistical mechanics,
 this equipartition law this equipartition law
 can be generalized can be generalized
 to be said that to be said that
 the average kinetic energy the average kinetic energy
 of each dynamical degree of of each dynamical degree of
 freedom is equal to freedom is equal to
 kT /2. kT /2.
 The proof of this theorem The proof of this theorem
 is given is given
 on the following page on the following page
 3-2-A:
Generalization of the Law of Equipartition of Energy
.
3-2-A:
Generalization of the Law of Equipartition of Energy
.

 But you may But you may
 skip this page, skip this page,
 if you feel it difficult or tedious if you feel it difficult or tedious
 because of mathematical because of mathematical
 formulae and complicated formulae and complicated
 expressions. expressions.

|
 [Heat Capacities of Gases] [Heat Capacities of Gases]

 Consider an ideal Consider an ideal
 (or perfect) gas. (or perfect) gas.
 It means a gas It means a gas
 in which the atomic in which the atomic
 or molecular interactions or molecular interactions
 can be neglected. can be neglected.
 In 1 mole In 1 mole
 of the gas, of the gas,
 there are there are
 as many molecules as many molecules
 as Avogadro's constant as Avogadro's constant
 NA. NA.

 In the case In the case
 of a monoatomic of a monoatomic
 molecular gas molecular gas
 like like
 a noble gas a noble gas
 (inert gas), (inert gas),
 the number of the degrees the number of the degrees
 of freedom of freedom
 of one molecule is 3, of one molecule is 3,
 which means the directions which means the directions
 of the of the
 x-, x-,
 y-, y-,
 and and
 z- axes. z- axes.
 Hence the total number Hence the total number
 of degrees of freedom of degrees of freedom
 in 1 mole of the gas in 1 mole of the gas
 is 3NA. is 3NA.

 An ordinary gas An ordinary gas
 like hydrogen or oxygen like hydrogen or oxygen
 is in general is in general
 diatomic molecular gas. diatomic molecular gas.
 In this case, In this case,
 as seen as seen
 in the following figure, in the following figure,
 there are 5 degrees of freedom; there are 5 degrees of freedom;
 3 of them are those 3 of them are those
 of the center-of-mass of the center-of-mass
 motion motion
 in the directions of the in the directions of the
 x-, x-,
 y-, y-,
 and and
 z- axes, z- axes,
 and the rest 2 and the rest 2
 are those of are those of
 the rotational motion the rotational motion
 around the center-of-mass, around the center-of-mass,
 i.e. the degrees of freedom of i.e. the degrees of freedom of

 and and
 . .
 Therefore the total number Therefore the total number
 of degrees of freedom of degrees of freedom
 in 1 mole of in 1 mole of
 a diatomic molecular gas a diatomic molecular gas
 is 5NA. is 5NA.

|


|
Degrees of freedom of a diatomic molecule

 Since there are Since there are
 2 degrees of freedom 2 degrees of freedom
 of the rotational motion, of the rotational motion,

 and and
 , ,
 of the rotational motion, of the rotational motion,
 in addition to in addition to
 3 degrees of freedom of the 3 degrees of freedom of the
 translational translational
 center-of-mass motion, center-of-mass motion,
 the total number the total number
 of degrees of freedom is 5. of degrees of freedom is 5.


|
 If we consider If we consider
 that the same amount that the same amount
 of kinetic energy of kinetic energy
 kT /2 kT /2
 is partitioned is partitioned
 onto these onto these
 3NA 3NA
 or or
 5NA 5NA
 degrees of freedom degrees of freedom
 according to the law according to the law
 of equipartition of energy, of equipartition of energy,
 the total energy E the total energy E
 of 1 mole of the gas of 1 mole of the gas
 would be would be



 Accordingly, the molar Accordingly, the molar
 heat capacities heat capacities
 (heat capacities per mole) (heat capacities per mole)
 of gases are of gases are



 These theoretical results These theoretical results
 are compared are compared
 with the experimental data with the experimental data
 in the following Table 1. in the following Table 1.


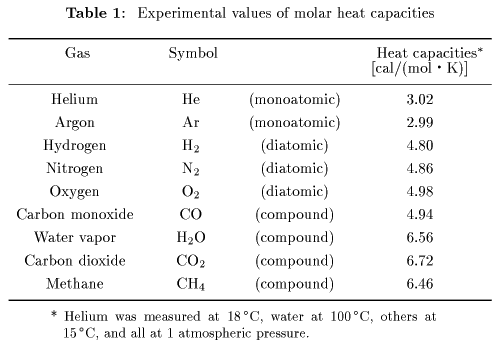
 We can see We can see
 from Table 1 that from Table 1 that
 the law of equipartition the law of equipartition
 of energy of energy
 is well satisfied. is well satisfied.
 The molecular structure The molecular structure
 of carbon monoxide resembles of carbon monoxide resembles
 to that of oxygen, to that of oxygen,
 so that those molar so that those molar
 heat capacities are heat capacities are
 rather similar rather similar
 to each other. to each other.
 However the molecular structures However the molecular structures
 of carbon dioxide, of carbon dioxide,
 water and methane water and methane
 are more complicated are more complicated
 than such a diatomic molecule than such a diatomic molecule
 as oxygen, as oxygen,
 and their heat capacities and their heat capacities
 appear to differ a little. appear to differ a little.

|
 [Heat Capacities of Solids]
[Heat Capacities of Solids]

 In a solid, In a solid,
 the inter-molecular interaction the inter-molecular interaction
 is so strong is so strong
 that the molecules that the molecules
 cannot freely move. cannot freely move.
 Therefore we cannot Therefore we cannot
 count the number count the number
 of degrees of freedom of degrees of freedom
 as done in a gas or liquid. as done in a gas or liquid.

|


|
 A Collection A Collection
 of Springs of Springs

 A solid is considered A solid is considered
 to be a collection to be a collection
 of oscillators. of oscillators.
 This figure is drawn This figure is drawn
 on a two-dimensional plane, on a two-dimensional plane,
 but but
 it should be noted it should be noted
 that a realistic solid that a realistic solid
 is is
 three-dimensional. three-dimensional.


|
 It is considered It is considered
 that each molecule that each molecule
 in a solid in a solid
 connects with adjacent ones connects with adjacent ones
 via springs as shown via springs as shown
 in the above figure. in the above figure.
 These molecules These molecules
 are infinitesimally oscillating are infinitesimally oscillating
 around their equilibrium around their equilibrium
 positions. positions.
 Namely, Namely,
 we can consider we can consider
 that there are that there are
 as many harmonic oscillators as many harmonic oscillators
 as the number of molecules as the number of molecules
 in the solid. in the solid.
 One molecule has One molecule has
 three directions of motion, three directions of motion,
 i.e. the directions of the i.e. the directions of the
 x-, x-,
 y- y-
 and and
 z- axes, z- axes,
 so that we can consider so that we can consider
 that there are that there are
 3NA 3NA
 harmonic oscillators harmonic oscillators
 in 1 mole of solid. in 1 mole of solid.
 As stated As stated
 on the page, on the page,
 3-2-A:
Generalization of the Law
of Equipartition of Energy,
3-2-A:
Generalization of the Law
of Equipartition of Energy,

 the constant amount the constant amount
 of energy kT of energy kT
 is partitioned is partitioned
 to every harmonic oscillator. to every harmonic oscillator.
 Hence the total energy Hence the total energy
 of a solid is of a solid is



 and and
 the molar heat capacity the molar heat capacity
 of a solid is of a solid is



 This result is This result is
 nothing other than nothing other than
 Dulong and Petit's law Dulong and Petit's law
 discovered experimentally discovered experimentally
 in 1819. in 1819.
 Some experimental data Some experimental data
 of molar heat capacities of molar heat capacities
 of solids of solids
 are shown are shown
 in Table 2. in Table 2.



|
 [Problems on Heat Capacities] [Problems on Heat Capacities]

 As discussed above, As discussed above,
 the molar heat capacities the molar heat capacities
 appear to be explained appear to be explained
 well by using well by using
 the law of equipartition the law of equipartition
 of energy. of energy.
 Certainly, Certainly,
 there is no problem there is no problem
 when the temperature when the temperature
 of the system of the system
 is high, is high,
 whereas problems might whereas problems might
 appear when the temperature appear when the temperature
 becomes low. becomes low.
 For example, For example,
 as seen in as seen in
 the following figure, the following figure,
 the molar heat capacity the molar heat capacity
 of zinc of zinc
 becomes smaller and smaller becomes smaller and smaller
 and approaches 0 and approaches 0
 when the temperature when the temperature
 comes close to 0 K. comes close to 0 K.
 Every solid shows Every solid shows
 a similar property. a similar property.
 This is a serious problem This is a serious problem
 that can never that can never
 be explained be explained
 with the classical theory. with the classical theory.



|
 Top
Top
|
|

 Go back to
the top page of Part 3. Go back to
the top page of Part 3.

 Go back to
the last page. Go back to
the last page.

 Go to
the next page. Go to
the next page.
|