
 Top of Part 4
Top of Part 4

 Last page
Last page

 Next page
Next page
  Top of Part 4
Top of Part 4
  Last page
Last page
  Next page
Next page
|
4-3: The Bohr Model of Atoms |
 The Rutherford model The Rutherford model
 of the nuclear atom of the nuclear atom
 had been beautifully had been beautifully
 successful in explaining successful in explaining
 the alpha particle scattering. the alpha particle scattering.
 It was however It was however
 completely powerless completely powerless
 to explain the stability to explain the stability
 of atoms and of atoms and
 to derive the atomic spectra. to derive the atomic spectra.
 As seen in the previous sections, As seen in the previous sections,
 it brought about it brought about
 a serious difficulty a serious difficulty
 which cannot be overcome which cannot be overcome
 within the classical theory. within the classical theory.

|


|
 Discussing Discussing
 with Rutherford in UK, with Rutherford in UK,
 N. H. D. Bohr N. H. D. Bohr
 (Denmark, 1885 - 1962) (Denmark, 1885 - 1962)
 learned the Rutherford model learned the Rutherford model
 and extended and extended
 this model to the so-called this model to the so-called
 Bohr model. Bohr model.

 Bohr Bohr
 followed Rutherford and followed Rutherford and
 thought that, thought that,
 in a hydrogen atom, in a hydrogen atom,
 an electron revolves an electron revolves
 about the proton about the proton
 at such speed at such speed
 that the Coulomb force that the Coulomb force
 between the electron between the electron
 and proton becomes and proton becomes
 just equal to the just equal to the
 centrifugal force centrifugal force
 to keep this orbital motion. to keep this orbital motion.

 As discussed As discussed
 on the preceding page, on the preceding page,
 this model this model
 was unstable with respect was unstable with respect
 to the classical theory. to the classical theory.
 Moreover, this model Moreover, this model
 had one more difficulty. had one more difficulty.
 It was known It was known
 that all hydrogen atoms that all hydrogen atoms
 are equal to each other are equal to each other
 and have the equal radius, and have the equal radius,
 but there was nothing but there was nothing
 in this model to assure in this model to assure
 this equality. this equality.
 Thus, if the Rutherford model Thus, if the Rutherford model
 was to survive, was to survive,
 it was necessary to find it was necessary to find
 a radical remedy a radical remedy
 that would bring that would bring
 both the stability and the both the stability and the
 constant radius. constant radius.

|
 To prepare the remedy, To prepare the remedy,
 taking a hint from taking a hint from
 Balmer's formula
Balmer's formula

 of the hydrogen spectra, of the hydrogen spectra,
 Bohr added the hypotheses Bohr added the hypotheses
 stated below to stated below to
 the Rutherford model the Rutherford model
 (1913). (1913).
 This model is This model is
 sometimes called sometimes called
 the Bohr-Rutherford model the Bohr-Rutherford model
 of the nuclear atom of the nuclear atom
 or Bohr's quantum theory, or Bohr's quantum theory,
 which was the first unified which was the first unified
 theory to be able theory to be able
 to explain the to explain the
 structure of the hydrogen atom structure of the hydrogen atom
 including both the stability including both the stability
 and the fixed radius. and the fixed radius.

[Bohr's Quantum Theory] 
 Bohr considered Bohr considered
 that the electrons revolve that the electrons revolve
 around the atomic nucleus around the atomic nucleus
 obeying the classical theory obeying the classical theory
 (Newtonian mechanics (Newtonian mechanics
 and Maxwellian electromagnetism). and Maxwellian electromagnetism).
 He added the following He added the following
 hypotheses hypotheses
 to the Rutherford model: to the Rutherford model:

|
 (1) (1)

|
 An atom can exist An atom can exist
 only in special states only in special states
 with discrete with discrete
 (step-like) (step-like)
 values of energy. values of energy.
 (Electrons in an atom (Electrons in an atom
 can exist only can exist only
 in certain special orbits.) in certain special orbits.)
 Bohr called these Bohr called these
 special states special states
 (or orbits) (or orbits)
 stationary states. stationary states.

|
|
 (2) (2)

|
 When an atom makes a When an atom makes a
 transition transition
 from one stationary state from one stationary state
 to another, to another,
 it emits or absorbs it emits or absorbs
 radiation whose radiation whose
 frequency frequency
 , ,
 is given by is given by
 the frequency condition the frequency condition




 where where
 E' and E'' E' and E''
 are the energies are the energies
 of these stationary states. of these stationary states.

|
|
 (3) (3)

|
 In the stationary states, In the stationary states,
 the electrons move the electrons move
 obeying obeying
 the classical theory. the classical theory.
 Among the possible motions Among the possible motions
 obeying the classical theory, obeying the classical theory,
 only those satisfying only those satisfying
 the following the following
 quantum condition
quantum condition
 are realized: are realized:




 where where
 p is p is
 the momentum of the electron the momentum of the electron
 and q is its and q is its
 coordinate variable. coordinate variable.
 The integration should The integration should
 be done along the orbit be done along the orbit
 over one period over one period
 of the cyclic motion. of the cyclic motion.

|
 The theory constructed The theory constructed
 on the basis of on the basis of
 the above hypotheses the above hypotheses
 is called is called
 Bohr's quantum theory Bohr's quantum theory
 or sometimes or sometimes
 the old quantum theory. the old quantum theory.

|
 [The Hydrogen Atom] [The Hydrogen Atom]

 Let us apply Let us apply
 Bohr's quantum theory Bohr's quantum theory
 to the hydrogen atom. to the hydrogen atom.

 Suppose that an electron Suppose that an electron
 (mass = m) (mass = m)
 revolves revolves
 around the proton around the proton
 being at rest at the center being at rest at the center
 under a Coulomb attractive force. under a Coulomb attractive force.
 This motion This motion
 of the electron of the electron
 is described is described
 by the Newtonian equation by the Newtonian equation
 of motion. of motion.
 The orbit of the electron The orbit of the electron
 in this case in this case
 is elliptic in general. is elliptic in general.
 Now, let us assume Now, let us assume
 it to be a circle it to be a circle
 for simplicity. for simplicity.
 In this case the absolute value In this case the absolute value
 of the momentum of of the momentum of
 the electron, p, the electron, p,
 is constant. is constant.
 Then the quantum condition Then the quantum condition
 is written is written




 where a where a
 is the radius of the orbit. is the radius of the orbit.

 From the balance From the balance
 of the centrifugal force of the centrifugal force
 and the Coulomb force, and the Coulomb force,
 we have we have




 Combining Eqs. (3) and (4), Combining Eqs. (3) and (4),
 we obtain the radius we obtain the radius
 a of the orbit as a of the orbit as




 Since the energy Since the energy
 of the electron, of the electron,
 E, is the sum of E, is the sum of
 the kinetic and potential the kinetic and potential
 energies, we have energies, we have




 Let us write this Let us write this
 En. En.

 The allowed energies The allowed energies
 of the hydrogen atom are of the hydrogen atom are
 the discrete ones the discrete ones
 , ,
 given by given by
 Eq. (6). Eq. (6).
 The state of n = 1 The state of n = 1
 is the lowest energy state is the lowest energy state
 called the ground state. called the ground state.
 The radius of the orbit The radius of the orbit
 in the ground state, a0, in the ground state, a0,
 is especially called the is especially called the
 Bohr radius, Bohr radius,
 whose value is whose value is




 This Bohr radius This Bohr radius
 is thought to be the radius is thought to be the radius
 of an ordinary hydrogen atom, of an ordinary hydrogen atom,
 and there can exist and there can exist
 no hydrogen atom no hydrogen atom
 with a radius smaller with a radius smaller
 than this. than this.

 When the hydrogen atom When the hydrogen atom
 jumps (makes a transition) jumps (makes a transition)
 from one stationary state from one stationary state
 with the energy with the energy
 En En
 to another with to another with
 Ek, Ek,
 it emits or absorbs it emits or absorbs
 a light whose frequency a light whose frequency
 , ,
 is given by is given by
 the frequency condition the frequency condition
 Eq. (1). Eq. (1).
 Using the energy Using the energy
 Eq. (6), Eq. (6),
 we therefore have we therefore have




 This is just the same as This is just the same as
 Balmer's Formula Balmer's Formula
 or or
 Rydberg's formula Rydberg's formula
 which was obtained which was obtained
 empirically. empirically.
 Therefore, the value Therefore, the value
 of the Rydberg constant of the Rydberg constant
 is calculated as is calculated as




 This result is exactly This result is exactly
 fit to the experimental value. fit to the experimental value.

 Thus, Bohr's quantum theory Thus, Bohr's quantum theory
 could beautifully reproduce could beautifully reproduce
 the structure of the structure of
 the hydrogen atom. the hydrogen atom.

|
 [The Energy Levels and [The Energy Levels and
 the Spectra of Hydrogen] the Spectra of Hydrogen]

 According to Bohr's According to Bohr's
 quantum theory, quantum theory,
 the energy of the hydrogen atom the energy of the hydrogen atom
 is given by Eq. (6). is given by Eq. (6).
 The state of n = 1 The state of n = 1
 is the ground state is the ground state
 which has the lowest energy. which has the lowest energy.
 The states of The states of
 n = 2, 3, ... n = 2, 3, ...
 are the excited states. are the excited states.
 These energy levels These energy levels
 are graphed in are graphed in
 the following figure the following figure
 in units of eV, in units of eV,
 where the energy E = 0 where the energy E = 0
 corresponds to the ionized corresponds to the ionized
 state of hydrogen state of hydrogen
 with the free electron at rest. with the free electron at rest.
 (The ionized state (The ionized state
 means the state in which means the state in which
 the hydrogen nucleus, the hydrogen nucleus,
 i.e. proton, i.e. proton,
 and the electron are and the electron are
 completely separated.) completely separated.)

|
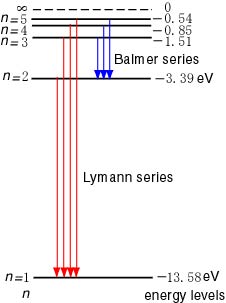
|
 The Energy Levels of Hydrogen
The Energy Levels of Hydrogen

 The state of n = 1 The state of n = 1
 is the ground state, and is the ground state, and
 n = 2, 3, ... are n = 2, 3, ... are
 the excited states. the excited states.
 The energies are The energies are
 in units of eV, in units of eV,
 being so measured being so measured
 that the completely ionized state that the completely ionized state
 is made to be of 0 eV. is made to be of 0 eV.

|
 The detailed experimental The detailed experimental
 data of the spectrum data of the spectrum
 of hydrogen are shown of hydrogen are shown
 in the following in the following
 figure, figure,
 where the Lymann, Balmer, where the Lymann, Balmer,
 Paschen and Brackett series Paschen and Brackett series
 are represented. are represented.
 As seen in the As seen in the
 above figure, above figure,
 these groups of spectral lines these groups of spectral lines
 are considered to are considered to
 correspond to the correspond to the
 radiations emitted when radiations emitted when
 the transitions occur the transitions occur
 from various states from various states
 to some specified state. to some specified state.




|
 [The Confirmation [The Confirmation
 of the Stationary States] of the Stationary States]

 In Bohr's quantum theory In Bohr's quantum theory
 (or the Bohr model of atoms), (or the Bohr model of atoms),
 Bohr postulated that Bohr postulated that
 an atom can exist only an atom can exist only
 in the stationary states in the stationary states
 with discrete with discrete
 (step-like) (step-like)
 values of energy. values of energy.
 This postulation This postulation
 is quite difficult is quite difficult
 to be understood to be understood
 with the classical theory. with the classical theory.
 However, the spectrum However, the spectrum
 of the hydrogen atom of the hydrogen atom
 could be reproduced could be reproduced
 beautifully. beautifully.
 This means that the idea This means that the idea
 of the stationary states of the stationary states
 appears "correct". appears "correct".

 Therefore people Therefore people
 wanted to confirm wanted to confirm
 the existence of the existence of
 the stationary states the stationary states
 directly by experiment. directly by experiment.
 This is the famous This is the famous
 Franck-Hertz experiment, Franck-Hertz experiment,
 which was carried out by which was carried out by
 J. Franck J. Franck
 (Germany, USA, 1882 - 1964) (Germany, USA, 1882 - 1964)
 and and
 G. Hertz G. Hertz
 (Germany, 1887 - 1975). (Germany, 1887 - 1975).

|
 This Hertz This Hertz
 is a researcher is a researcher
 different from different from
 H. R. Hertz H. R. Hertz
 (Germany, 1857 - 94) (Germany, 1857 - 94)
 who was famous who was famous
 for the research for the research
 on electromagnetic waves on electromagnetic waves
 in the 19th century. in the 19th century.

|
 A schematic drawing A schematic drawing
 of the apparatus of the apparatus
 used by Franck and Hertz used by Franck and Hertz
 is shown in the following is shown in the following
 Fig. (A). Fig. (A).
 Low-pressure mercury vapor Low-pressure mercury vapor
 is introduced in a tube, is introduced in a tube,
 in which a filament F in which a filament F
 is heated up is heated up
 and electrons are and electrons are
 emitted from it. emitted from it.
 The emitted electrons The emitted electrons
 are accelerated toward are accelerated toward
 the grid G the grid G
 by the electric potential by the electric potential
 between the filament F between the filament F
 and the grid G, and the grid G,
 and after passing through and after passing through
 the grid have a the grid have a
 kinetic energy eV. kinetic energy eV.
 Then the electrons Then the electrons
 are subjected to a small are subjected to a small
 retarding potential retarding potential

 before being collected before being collected
 on the plate P. on the plate P.




 If an electron loses If an electron loses
 no energy in the course no energy in the course
 from the filament to from the filament to
 the grid, the grid,
 it will arrive it will arrive
 at the plate with the energy at the plate with the energy

 and contribute to and contribute to
 the current measured the current measured
 by the ammeter A. by the ammeter A.
 However, if However, if
 eV eV
 is greater than is greater than
 the excitation energy the excitation energy
 of the gas atom of the gas atom
 from the ground state from the ground state
 to the first excited state, to the first excited state,
 some of the electrons some of the electrons
 will lose a part will lose a part
 of the kinetic energy of the kinetic energy
 on colliding on colliding
 with a gas atom. with a gas atom.
 Then they have insufficient Then they have insufficient
 energy left to overcome the energy left to overcome the
 retarding potential retarding potential

 Consequently, as the potential Consequently, as the potential
 V V
 is increased gradually, is increased gradually,
 we can find we can find
 a quick drop a quick drop
 of the current measured with of the current measured with
 the ammeter A, the ammeter A,
 when the energy eV when the energy eV
 is equal to the is equal to the
 excitation energy excitation energy
 of the gas atom. of the gas atom.
 If the potential V If the potential V
 is then increased again, is then increased again,
 the current should rise, the current should rise,
 and the second drop and the second drop
 would appear when eV would appear when eV
 is equal to twice the is equal to twice the
 excitation energy. excitation energy.

 In 1914, In 1914,
 Franck and Hertz Franck and Hertz
 demonstrated such demonstrated such
 energy absorption energy absorption
 whose experimental data whose experimental data
 is shown in the is shown in the
 above Fig. (B). above Fig. (B).
 As the potential V As the potential V
 between the filament between the filament
 and the grid and the grid
 is raised, the current is raised, the current
 gradually increases, gradually increases,
 but suddenly decreases but suddenly decreases
 at V at V
 = 4.9V. = 4.9V.
 After that, the current After that, the current
 increases again and increases again and
 the second drop appears the second drop appears
 at V at V
 = 9.8V, = 9.8V,
 and the similar phenomena and the similar phenomena
 are repeated. are repeated.

 This means that This means that
 the excitation energy the excitation energy
 of the mercury atom of the mercury atom
 should be 4.9 eV. should be 4.9 eV.
 It was confirmed It was confirmed
 that this excitation energy that this excitation energy
 was just equal was just equal
 to that obtained to that obtained
 from the spectra of mercury. from the spectra of mercury.

 Franck and Hertz Franck and Hertz
 obtained similar obtained similar
 experimental results experimental results
 using not only mercury using not only mercury
 but also neon, argon, but also neon, argon,
 krypton and so on. krypton and so on.
 These results would be These results would be
 the experimental proofs the experimental proofs
 of the Bohr's postulation of the Bohr's postulation
 of the of the
 stationary states. stationary states.

|
 Top
Top
|
|

 Go back to
the top page of Part 3. Go back to
the top page of Part 3.

 Go back to
the last page. Go back to
the last page.

 Go to
the next page. Go to
the next page.
|