
 Top Part 1
Top Part 1

 Next page
Next page
  Top Part 1
Top Part 1
  Next page
Next page
|
1-1: Bohr's Quantum Theory and De Broglie Waves |
 [Bohr's Quantum Theory] [Bohr's Quantum Theory]
 We learned on We learned on
 the page, the page,
 4-3: The Bohr Model of Atoms
4-3: The Bohr Model of Atoms
 in the preceding Seminar, in the preceding Seminar,
 that that
 the atomic structure the atomic structure
 of hydrogen of hydrogen
 that had been difficult that had been difficult
 to be understood to be understood
 with classical theory with classical theory
 was beautifully explained was beautifully explained
 by Bohr's quantum theory. by Bohr's quantum theory.
 This theory This theory
 is sometimes called is sometimes called
 the old quantum theory. the old quantum theory.

 Here let us summarize Here let us summarize
 the main points the main points
 of the theory. of the theory.
 In Bohr's quantum theory, In Bohr's quantum theory,
 it is considered it is considered
 that an atom that an atom
 can be described by can be described by
 the Rutherford model of the nuclear atom,
the Rutherford model of the nuclear atom,
 in which a heavy nucleus in which a heavy nucleus
 is surrounded by is surrounded by
 light electrons light electrons
 that move obeying that move obeying
 the classical theory. the classical theory.
 Since this atomic model Since this atomic model
 brought about brought about
 some difficulties some difficulties
 discussed on discussed on
 the pages, the pages,
 2-7: Summary of Part 2
2-7: Summary of Part 2
 and and
 4-1: The Difficulty of the Rutherford Model of the Nuclear Atom
4-1: The Difficulty of the Rutherford Model of the Nuclear Atom
 in the preceding Seminar, in the preceding Seminar,
 Bohr added the Bohr added the
 following hypotheses; following hypotheses;
 i.e., i.e.,
 postulations of postulations of
 stationary state, stationary state,
 frequency condition, frequency condition,
 and and
 quantum condition. quantum condition.

 A schematic sketch of A schematic sketch of
 the Rutherford model the Rutherford model
 of the nuclear atom of the nuclear atom
 is represented in is represented in
 the following figure, the following figure,
 in which in which
 the central black sphere the central black sphere
 is the atomic nucleus, is the atomic nucleus,
 and the small points and the small points
 denote the electrons denote the electrons
 surrounding the nucleus. surrounding the nucleus.
 While the atomic radius While the atomic radius
 is about is about
 , ,
 the nuclear radius the nuclear radius
 seems to be less seems to be less
 than 1/10000 of it. than 1/10000 of it.

|

|
 The Rutherford Model of the Nuclear Atom
The Rutherford Model of the Nuclear Atom

 A black big ball A black big ball
 at the center at the center
 is the nucleus and is the nucleus and
 small red points moving small red points moving
 around the nucleus around the nucleus
 are electrons. are electrons.

|
 By Bohr's By Bohr's
 Quantum theory, Quantum theory,
 the structure, the structure,
 especially the energy, especially the energy,
 the radius, the stability the radius, the stability
 and the spectra and the spectra
 of hydrogen atom, of hydrogen atom,
 were explained were explained
 very well. very well.

|


|
 [De Broglie Waves] [De Broglie Waves]

 As mentioned previously, As mentioned previously,
 it was clarified it was clarified
 by the discovery of by the discovery of
 the photon the photon
 that light that light
 which had so far which had so far
 been considered been considered
 to be wave to be wave
 (electromagnetic wave) (electromagnetic wave)
 has also a particle nature. has also a particle nature.
 Then de Broglie Then de Broglie
 (France, 1892 - 1987) (France, 1892 - 1987)
 thought that thought that
 such things as such things as
 electrons which electrons which
 had so far been considered had so far been considered
 to be particles to be particles
 might possess wave nature might possess wave nature
 as well (1932). as well (1932).
 This is the idea This is the idea
 of the de Broglie waves of the de Broglie waves
 or de Broglie's or de Broglie's
 matter waves. matter waves.

 We know that, We know that,
 in the case of light, in the case of light,
 the frequency the frequency
 , ,
 and the wavelength and the wavelength
 , ,
 are connected respectively to are connected respectively to
 the energy E the energy E
 and the momentum p and the momentum p
 of photon of photon
 by means of by means of
 Einstein's relations Einstein's relations

|



 De Broglie assumed that De Broglie assumed that
 these relations (1) these relations (1)
 might be valid might be valid
 also for the de Broglie waves. also for the de Broglie waves.
 The above Einstein's The above Einstein's
 relations are relations are
 therefore called therefore called
 Einstein - de Broglie's Einstein - de Broglie's
 relations as well. relations as well.

|
 [The Evidences of De Broglie Waves] [The Evidences of De Broglie Waves]
 C. J. Davisson C. J. Davisson
 (USA, 1881 - 1958) (USA, 1881 - 1958)
 and and
 L. H. Germer L. H. Germer
 (USA, 1896 - 1971) (USA, 1896 - 1971)
 observed the interference observed the interference
 phenomena resulting from phenomena resulting from
 an electron beam an electron beam
 reflected from reflected from
 a single crystal of nickel, a single crystal of nickel,
 and they confirmed and they confirmed
 that the interference that the interference
 was a perfect fit to was a perfect fit to
 Einstein-de Broglie's relations. Einstein-de Broglie's relations.
 At the same time, At the same time,
 G. P. Thomson G. P. Thomson
 (UK, 1892 - 1975) (UK, 1892 - 1975)
 also confirmed also confirmed
 the wave nature of electrons the wave nature of electrons
 using a metallic multi-crystal. using a metallic multi-crystal.
 (See the photograph of
a diffraction pattern of electron beams (See the photograph of
a diffraction pattern of electron beams
 on the page, on the page,
 4-4: in the preceding Seminar). 4-4: in the preceding Seminar).

 Moreover, Moreover,
 O. Stern O. Stern
 (Germany, 1888 - 1969) (Germany, 1888 - 1969)
 observed the interference patterns observed the interference patterns
 produced by projecting produced by projecting
 beams of helium atoms beams of helium atoms
 and hydrogen molecules and hydrogen molecules
 onto crystals, onto crystals,
 and confirmed that and confirmed that
 the results exactly the results exactly
 fit the fit the
 Einstein-de Broglie's relations. Einstein-de Broglie's relations.
 Thereby Thereby
 de Broglie waves accompanying de Broglie waves accompanying
 not only electrons but not only electrons but
 also also
 general particles general particles
 were confirmed were confirmed
 experimentally. experimentally.

|
 [Bohr's Quantum Condition [Bohr's Quantum Condition
 and De Broglie Waves] and De Broglie Waves]

 Let us consider Let us consider
 a hydrogen atom with a hydrogen atom with
 Bohr's quantum theory. Bohr's quantum theory.
 In that theory, In that theory,
 the quantum condition the quantum condition
 to determine the to determine the
 stationary states stationary states
 of the atom of the atom
 seems to claim seems to claim
 that the circumference that the circumference
 of the orbit of the electron of the orbit of the electron
 revolving about the nucleus revolving about the nucleus
 should be an integral multiple should be an integral multiple
 of the wavelength of the wavelength
 of the de Broglie wave of the de Broglie wave
 of the electron. of the electron.
 This has already been discussed This has already been discussed
 on the page, on the page,
 4-4: The Wave Nature of Electrons
4-4: The Wave Nature of Electrons
 in the preceding Seminar. in the preceding Seminar.
 This quantum condition This quantum condition
 says that says that
 the de Broglie wave the de Broglie wave
 of the electron must be of the electron must be
 a continuous a continuous
 standing wave standing wave
 around the nucleus. around the nucleus.
 (See the following (See the following
 figure.) figure.)

|
|
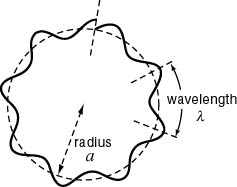
 Bohr's quantum condition Bohr's quantum condition
 for a hydrogen atom. for a hydrogen atom.

 In this figure, In this figure,
 the de Broglie wave the de Broglie wave
 does not connect smoothly, does not connect smoothly,
 because the circumference because the circumference
 is not an integral multiple is not an integral multiple
 of the wave length. of the wave length.
 Namely, this figure Namely, this figure
 does not show does not show
 a correct de Broglie wave a correct de Broglie wave
 in a hydrogen atom. in a hydrogen atom.
 The circumference The circumference
 of a true hydrogen atom of a true hydrogen atom
 must be must be
 an integral multiple an integral multiple
 of the de Broglie wavelength. of the de Broglie wavelength.

|
 We can easily We can easily
 understand and explain understand and explain
 this quantum condition this quantum condition
 by considering by considering
 the smooth continuity the smooth continuity
 of the de Broglie waves. of the de Broglie waves.
 Thus we can realize that Thus we can realize that
 the de Broglie waves the de Broglie waves
 play an essential role play an essential role
 underlying Bohr's underlying Bohr's
 quantum theory. quantum theory.
 They looked forward to They looked forward to
 construction of construction of
 a really new theory a really new theory
 from which Bohr's quantum from which Bohr's quantum
 theory itself theory itself
 can be derived inevitably. can be derived inevitably.
 Such a theory is Such a theory is
 nothing other than nothing other than
 Schroedinger's wave mechanics Schroedinger's wave mechanics
 or quantum mechanics. or quantum mechanics.

|
 Top
Top
|
 Go back to
the top page of Part 2. Go back to
the top page of Part 2.

 Go to
the next page. Go to
the next page.
|